6. Однофакторный дисперсионный анализ

Однофакторный дисперсионный анализ проводится для выявления влияния одной переменной на другую. При этом одна из переменных является независимой и должна быть порядковой или номинальной. А другая — зависимой и метрической. Данный вид анализа проверяет верность гипотезы, согласно которой средние величины более чем в двух группах равны [1].

С помощью однофакторного дисперсионного анализа можно найти ответы, например, на следующие вопросы:

1. Действительно ли различаются предпочтения потребителей к торговой марке в зависимости от их уровня дохода;
2. Действительно ли различаются предпочтения потребителей к торговой марке в зависимости от вида рекламного ролика, который они посмотрели;
3. Различаются ли группы потребителей по предпочтениям мест приобретения товара;
4. Влияет ли уровень образования респондентов на выбор мета отдыха;
5. Различаются ли географические сегменты по товарным предпочтениям потребителей.

При однофакторном дисперсионном анализе сравниваются между собой средние значения нескольких групп (выборок), на которые делятся все анализируемые данные. Независимая переменная, при помощи которой все данные разделяются на группы (категории) называется категориальным фактором (Рисунок 6.1).

Рисунок 6.1 — Диалоговое окно Однофакторного дисперсионного анализа

Последовательность проведения однофакторного дисперсионного анализа:

1. Формулировка вопроса в соответствии с требованиями, предъявляемыми к переменным, выбор зависимой и независимой переменных.
2. Формулирование исходной (нулевой гипотезы), согласно которой нет связи между выбранными переменными. В результате анализа нулевая гипотеза должна быть подтверждена или опровергнута.
3. В ходе проведения анализа проверяются условия равенства дисперсий зависимой переменной в нескольких выбранных группах (категориях).
4. Проведение проверки неравенства средних значений зависимой переменной в сравниваемых группах для выявления взаимосвязи между переменными.
5. Определение особенностей выявленной взаимосвязи, выявление категорий ее обуславливающих.

Пример. Используя базу данных опроса отдыхающих базы отдыха “Солнечная” проверим, существует ли взаимосвязь между доходом отдыхающих и суммой, которую они готовы потратить на 1 человека за 1 сутки отдыха за городом.

Предварительно перед проведением однофакторного дисперсионного анализа проведем преобразование данных о среднем доходе респондентов и создадим категориальную переменную “группы по доходу” с тремя значениями “низкий доход”, “средний доход”, “высокий доход”.

Нулевая гипотеза — туристы с разным уровнем дохода готовы потратить в среднем одинаковую сумму на 1 человека за 1 сутки отдыха за городом. (Не существует связи между доходом отдыхающих и размером суммы, которую они готовы потратить на отдых за городом)

Пошаговая инструкция

Шаг 1. Анализ — Сравнение средних — Однофакторный дисперсионный анализ

Шаг 2. “Общие расходы на отдых_сумма” в поле “Список зависимых переменных”

Шаг 3. “Группы по доходу” в поле “Фактор”

Шаг 4. Кнопка “Параметры— в открывшемся окне выбрать: Описательные, Проверка однородности дисперсии и График средних (Рисунок 6.2)

Рисунок 6.2 — Диалоговое окно “Описательные статистики”

Шаг 5. Кнопка “Продолжить”

Шаг 6. Кнопка “Апостериорные”: выбрать Шефе и Т2 Тамхейна (Рисунок 6.3)

Шаг 7. Кнопка “Продолжить” и ОК.

Рисунок 6.3 — Апостериорные множественные сравнения

Вверх

Интерпретация результатов

Проверка практической значимости результатов исследования.

На экран компьютера выводится таблица “Описательные статистики”, которая содержит статистические показатели, описывающие распределение зависимой переменной в разных группах. В данном примере таблица 6.1 содержит зависимую переменную “расходы на отдых” в группах отдыхающих с разным уровнем дохода.

Таблица 6.1 — Описательные статистики: расходы сумма

На данном этапе проверяется практическая значимость сформированных групп. Все группы имеют практическую значимость для исследования, так как количество объектов исследования в каждой группе больше 2. В случае, если сформируется группа с одним ответом респондента, эта группа должна быть исключена из исследования, так как является практически незначимой.

1. Проверка равенства дисперсий по тесту Ливиня.
   Проверяется гипотеза “Дисперсии в сравниваемых группах равны”. Значимость 0,333 означает, что гипотеза может быть отклонена с вероятностью ошибки 33%. Следовательно, гипотеза не отклоняется, и это значит, что дисперсии равны. Если значимость будет меньше 0,05, гипотеза может быть отклонена, то есть дисперсии не равны.

   Статистика Ливиня	Ст. св. 1	Ст. св. 2	Знч.
   1,129	2	42	,333

   Таблица 6.2 — Критерий однородности дисперсий: расходы сумма

   Критерий однородности дисперсий Ливиня со значимостью 0,333 показал, что дисперсии для каждой из групп статистически достоверно не различаются. Следовательно, результаты анализа корректны, в качестве апостериорных сравнений (множественных) будем использовать тест Шеффе.

2. Проверка верности нулевой гипотезы
   После проверки равенства дисперсий на экран выводятся результаты однофакторного дисперсионного анализа.

   	Сумма квадратов	Ст. св.	Средний квадрат	F	Знч.
   Между группами	6214056,16	2	3107028,08	27,38	,000
   Внутри групп	4765054,94	42	113453,68
   Итого	1,098E7	44

   Таблица 6.3 — Однофакторный дисперсионный анализ: расходы сумма

   Проверяем верность исходной нулевой гипотезы: туристы с разным уровнем дохода готовы потратить в среднем одинаковую сумму на 1 человека за 1 сутки отдыха за городом. (Не существует связи между доходом отдыхающих и размером суммы, которую они готовы потратить на отдых за городом).

   Она может быть отклонена с вероятностью ошибки 0% (значимость 0,000), то есть гипотеза не верна и должна быть отклонена.

   Следовательно, можно сделать вывод, что туристы с разным уровнем дохода готовы потратить разные суммы на 1 человека за 1 сутки отдыха за городом (существует зависимость между доходом отдыхающих и размером суммы, которую они готовы потратить на отдых за городом).

3. Для того, чтобы получить более точные результаты определим группы, в которых отличия наиболее значительны.

Проводим последующие многовариантные (множественные сравнения). В нашем случае дисперсии равны, поэтому анализируем данные теста Шеффе. В случае неравенства дисперсий значимыми являются данные теста Т2 Тамхейна.

Пары, характеризующиеся значительной разностью средних, обозначаются звездочкой.

Как видно из таблицы 6.4 разность сумм, которую готовы потратить на отдых туристы, значительна для каждой из групп.

Значимость в каждой группе меньше 0,05, что говорит о достоверности результатов анализа.

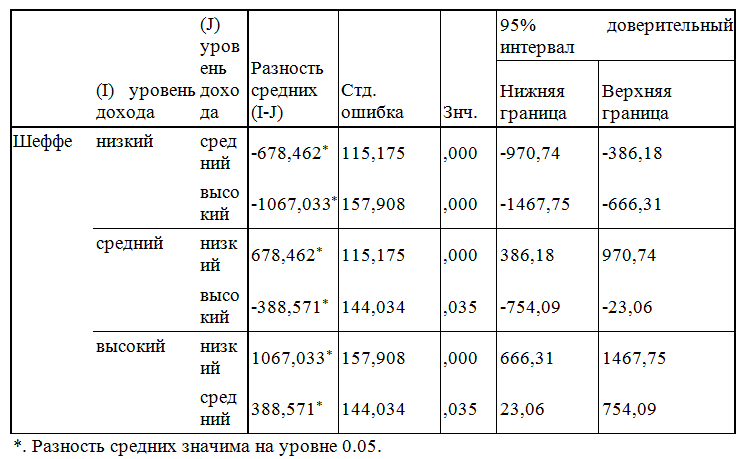
Таблица 6.4 — Множественные сравнения. Зависимая переменная: расходы сумма

*. Разность средних значима на уровне 0.05.

Значимость разности сумм, которую туристы с разным уровнем дохода готовы потратить на отдых за городом можно также увидеть на графике (рисунок 6.1).

Рисунок 6.4 — Зависимость средних расходов на отдых и уровнем дохода респондента

В целом можно сделать вывод, что как низкий, так и средний и высокий уровень дохода туриста влияет на размер суммы, которую он готов потратить на 1 человека за 1 день отдыха за городом. Следовательно, менеджменту базы отдыха “Солнечная” необходимо продумать грамотную политику ценообразования с учетом сегментирования рынка по доходу отдыхающих.