5. Сравнение средних величин

Методы сравнения средних величин часто используются в маркетинговых исследованиях для выявления взаимосвязи между исследуемыми переменными. К таким методам относятся T—тесты и дисперсионный анализ.[2]

Основные термины

Нулевая гипотеза — предположение о том, что между определенными статистическими параметрами генеральной совокупности не существует связи или различия. Ее подтверждение не требует от компании каких—либо действий [1].

Альтернативная гипотеза — утверждение о том, что между определенными статистическими параметрами генеральной совокупности есть связь или различия. Ее подтверждение означает, что руководству компании следует предпринять какие—либо действия или менять свои взгляды на положение дел [1].

Параметрические методы проверки гипотез — применяются для переменных, измеренных с помощью интервальных шкал.

Непараметрические методы проверки гипотез — применяются для переменных, измеренных с помощью номинальных или порядковых шкал.

Размах вариации R — это разность между самым большим и самым малым значениями признака у единиц данной совокупности: R=X_max — X_min

Дисперсия — это средний квадрат отклонений индивидуальных значений признака от его средней величины.

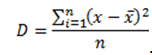
где D — дисперсия, x — анализируемый показатель, с черточкой сверху — среднее значение показателя, n — количество значений в анализируемой совокупности данных.

Стандартное отклонение — корень из дисперсии (среднего квадрата отклонений).

Коэффициент вариации — наиболее универсальных показатель, отражающий степень разбросанности значений независимо от их масштаба и единиц измерения. Коэффициент вариации измеряется в процентах и может быть использован для сравнения вариации различных процессов и явлений.

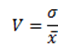
F—критерий или критерий Фишера — статистический критерий, с помощью которого проверяется гипотеза о равенстве дисперсий двух разных совокупностей. F—критерий это отношение двух выборочных дисперсий.

Т—критерий — Одномерный метод проверки гипотез, использующий Т—распределение. Т—критерий применяется для небольших выборок, когда стандартное отклонение не известно.

Метод Т—теста используется для проверки достоверности различия двух выборок по количественной переменной. Нулевая гипотеза формулируется следующим образом: “Взаимосвязи между исследуемыми переменными нет”. Например, формулируя исходную (нулевую) гипотезу предполагаем равенство среднего чека покупателей разного возраста, это говорит о том, что люди разного возраста в среднем тратят одинаковую сумму на покупки. В результате проведенного исследования данная гипотезе либо подтверждается, либо опровергается.

SPSS предлагает сравнивать средние величины при помощи нескольких методов (рисунок 5.1).

Рисунок 5.1 — Методы сравнения средних величин

Результат сравнения средних значений с применением Т—теста оценивается по уровню значимости (р—уровень). Значимость является мерой достоверности вычисленных результатов. Если “Значимость” не превышает 0,05, это означает, что нулевая (исходная) гипотеза может быть отклонена с вероятностью ошибки меньше 5%, т.е. ее можно отклонить и, следовательно, она неверна.

При использовании Т—теста устанавливается доверительный интервал равный 95%.

Рисунок 5.2 — Сравнение средних

При запуске процедуры “Сравнение средних” (рисунок 5.2) программа определяет средние показатели выбранных для анализа зависимых переменных в разных группах при помощи T—критерия.

Одновыборочный t—критерий используется для сравнения средней величины изучаемого признака в выборке с некоторой эталонной величиной. Например, отличается ли средняя цена на конкретный товар выбранных торговых предприятий от средней цены, рассчитанной официальным источником или ценой, которую готовы заплатить потребители за данный товар.

Т—критерий для независимых выборок (рисунок 5.1) используется для сравнения средних значений двух выборок. Для данных выборок должны быть определены значения одной и той же переменной. Например: удовлетворенность покупкой мужчин и женщин, семейных и несемейных, предпочитающих или не предпочитающих марку “АК” и т.д.

Т—критерий для парных выборок (рисунок 5.1) позволяет сравнить средние занчения двух измерений одного признака для одной и то же выборки. Например, результаты опроса потребителей в начале и в конце месяца.

В случае, когда необходимо сравнивать величины более чем в двух группах, применяется однофакторный дисперсионный анализ (рисунок 5.1).

Пример. Предположим, что было проведено маркетинговое исследование “Использование респондентами Интернета для личных целей”. В таблице 1 представлены данные о 30 респондентах, включающие пол (1—мужчина, 2—женщина), использование Интернета (в часах в неделю).

Вверх

Номер респондента	Пол	Использование Интернета
1	1.0	14.0
2	2.0	2.0/
3	2.0	3.0
4	2.0	3.0
5	1.0	13.0
6	2.0	6.0
7	2.0	2.0
8	2.0	6.0
9	2.0	6.0
10	1.0	15.0
11	2.0	3.0
12	2.0	4.0
13	1.0	9.0
14	1.0	8.0
15	1.0	5.0
16	2.0	3.0
17	1.0	9.0
18	1.0	4.0
19	1.0	14.0
20	2.0	6.0
21	1.0	9.0
22	1.0	5.0
23	2.0	2.0
24	1.0	15.0
25	2.0	6.0
26	1.0	13.0
27	2.0	4.0
28	2.0	2.0
29	1.0	4.0
30	1.0	3.0

Таблица 5.1 — Результаты маркетингового исследования

Проблема. Мы хотим определить, действительно ли мужчины более интенсивно используют Интернет, чем женщины. С этой целью проведем Т—тест для двух независимых выборок.

Т—тест позволяет проверить равенство средних значений тестируемого показателя в двух группах. В данном примере нулевую гипотезу формулируем следующим образом: “Мужчины и женщины одинаково часто пользуются Интернетом, т.е. пол не влияет на интенсивность пользования Интернетом”.

Пошаговая инструкция

Шаг 1. Меню “Анализ — Сравнение средних — Т—критерий для независимых выборок”. В окне “T—критерий для независимых выборок” выбираем метку тестируемой переменной (в рассматриваемом примере это “Использование Интернет”) и переносим ее в поле “Проверяемые переменные”. Далее выбираем метку группирующей переменной (в рассматриваемом примере это “Пол”) и переносим ее в поле “Группировать”.

Шаг 2. Кодируем группирующую переменную, создаем две группы: мужчины — присваиваем код“1”, женщины — код “2”.
Метрические переменные, например “возраст”, выбираются при помощи порогового значения, например, “Пороговое значение” — возраст 35 лет.

Шаг 3. “Продолжить— диалоговое окно “T—критерий для независимых выборок”.
“Параметры” — “Процент доверительного интервала”, который по умолчанию задается в размере 95%.

Шаг 4. “Продолжить” — диалоговое окно “Т—критерий для независимых выборок” — “ОК”

Рисунок 5.2 — Интерпретация результатов для независимых выборок

Верность выдвинутой гипотезы можно проверить с помощью величины “Значимость” по критерию Ливиня (рисунок 5.2), которая равна 0,000 (F—критерий имеет вероятность меньше 0,05). Следовательно, гипотезу о равенстве дисперсий отклоняем с вероятностью ошибки 0%, что ниже порогового значения 5%. Нулевая гипотеза (Но) отклоняется. Следовательно, в данном случае используется t—критерий, соответствующий утверждению “Равенство дисперсий не предполагается”. На рисунке 5.2 можно видеть, что t равно 4,492, степеней свободы — 18,014, двусторонняя значимость равна 0,000, которое меньше допустимого уровня, равного 0,05. Следовательно, гипотезу о том, что мужчины и женщины одинаково часто пользуются Интернет отклоняем. Поскольку среднее значение частоты использования Internet мужчинами равно 9,333, а женщинами — 3,867, то мужчины используют Internet значительно больше по сравнению с женщинами.

Обратный пример

Нулевая гипотеза –дисперсии распределения удовлетворенности мужчин и женщин равны (сравниваемые средние величины равны) — мужчины и женщины одинаково удовлетворены местом отдыха.

В таблице 5.2 выведены рассчитанные статистические показатели в исследуемых группах, которые представили 45 мужчин и 43 женщины. В среднем удовлетворенность местом отдыха у мужчин равна 2,34, а у женщин — 2,87.

Таблица 5.3 — Критерии для независимых выборок

С помощью T—теста определим с точки зрения статистики значимость разницы между уровнем удовлетворенности местом отдыха у мужчин и женщин.

При проведении теста Ливина проверяется следующая гипотеза: “Дисперсии распределения тестируемой величины в разных группах равны” [1]. Верность данной гипотезы определяется на основе величины “Significance” (“Значимость”). В зависимости от выполнения условия равенства дисперсий необходимо выбрать одну из строк таблицы. При заданной величине доверительного интервала 95% (вероятность ошибки в случае отклонения исходной гипотезы — 5%) значимость 0,158 (тест Ливиня), что > 0,05. Таким образом, гипотеза о равенстве дисперсий может быть отклонена с вероятностью ошибки 15,8%, что значительно больше допустимых 5%. Гипотеза не отклоняется, она верна — дисперсии равны.

Выбираем строку равенства дисперсий и проверяем верность гипотезы “Средние величины в двух группах равны”. Показатель Значимость (2—сторонняя) составляет 0,192, что означает, что гипотеза о том, что мужчины и женщины одинаково удовлетворены местом отдыха, может быть отклонена с вероятностью ошибки 19,2%, а это выше допустимого уровня в 5%. Следовательно, исходную гипотезу не отклоняем, сравниваемые величины с точки зрения статистики равны, и разница между средними уровнями удовлетворенности отдыхом у мужчин и женщин не является статистически значимой.

Таким образом, в результате проведенного Т—теста доказано, что удовлетворенность местом отдыха не зависит от пола туриста.