9. Кластерный анализ

Кластерный анализ — позволяет выявить группы (кластеры) объектов по заданным переменным. Программа при этом автоматически определяет количество существующих кластеров.

Задача кластерного анализа состоит в формировании групп:

С помощью кластерного анализа в маркетинге выявляются целевые группы потребителей, для которых необходимо разработать уникальный комплекс инструментов маркетинга.

Пример. Необходимо разделить всех курящих по возрасту и уровню дохода на однородные группы (кластеры) (рисунок 9.1).

На рисунке 9.1. вариант В не выявлено однородных кластеров, все курильщики представляют единю группу, следовательно, разработка уникальных торговых предложений не имеет смысла.

На рисунке 9.1. вариант А выявлены два однородных кластера курящих: “старые и бедные”, “молодые и богатые”. Данные группы могут быть представлены, как две целевые группы потребителей табачных изделий. Следовательно. Для каждой из них необходимо разработать уникальные торговые предложения по цене, качеству, особым свойствам, дизайну упаковки, особенностям продвижения, системе распределения товара.

Рисунок 9.1 — Кластерный анализ [2]

Рисунок 9.1 — Кластерный анализ [2]

В процессе выполнения кластерного анализа выявляются статистические связи между анализируемыми переменными, которые указывают на схожесть переменных и, затем объединение выявленных факторов в группы на основе уровня различий между ними. Количество кластеров зависит от задаваемых параметров схожести переменных, объединяемых в один кластер.

Основные термины, применяемые в кластерном анализе

Евклидово расстояние — расстояние между объектами, равное сумме квадратов разностей между значениями одноименных переменных объектов.

Иерархическая кластеризация — метод, при котором строится иерархическая или древовидная структура. Позволяет детально исследовать различия между объектами, выбрать оптимальное число кластеров.

Агломеративная или объединяющая кластеризация — иерархический метод формирования кластеров, при котором каждый объект сначала находится в отдельном кластере, затем объекты группируются в значительно более крупные кластеры.

Разделяющая или дивизиональная кластеризация — иерархический метод формирования кластеров, при котором один общий большой все кластер делится на более мелкие для создания однородных кластеров.

Методы связи — методы формирования кластеров, при которых объекты объединяются в группу на основе рассчитанного между ними расстояния (рисунок 9.2).

Метод одиночной связи — или правило ближайшего соседа — в основе лежит выбор переменных, расстояние между которыми минимально.

Метод полной связи — или правило дальнего соседа - в основе лежит выбор переменных, расстояние между которыми максимально.

Метод средней связи — в основе лежит среднее значение расстояния между переменными разных кластеров.

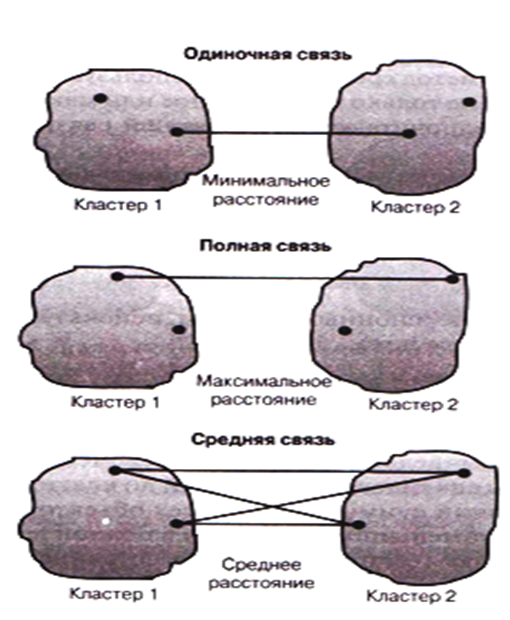
Рисунок 9.2 — Методы связи

Рисунок 9.2 — Методы связи

Дисперсионные методы — Метод Варда и Центроидный метод (Рисунок 9.3).

Метод Варда — в качестве меры используется квадрат евклидового расстояния, который должен быть минимальным.

Центроидный метод — оценивается расстояние между центроидами (средними) групп переменных.

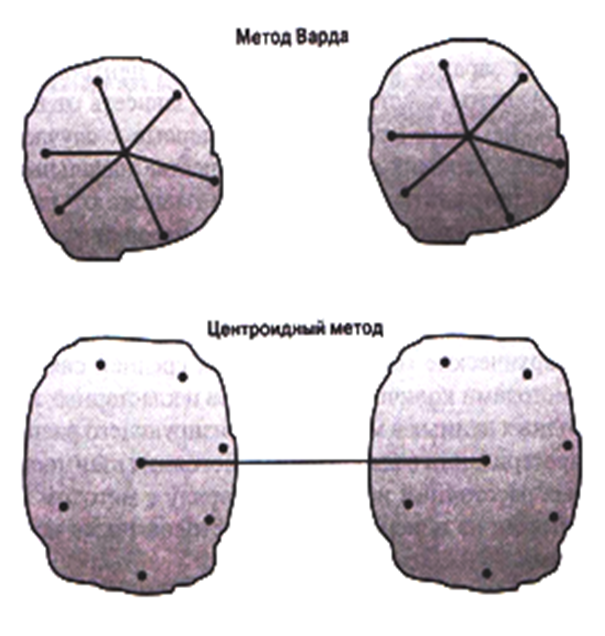
Рисунок 9.3 — Дисперсионные методы

Рисунок 9.3 — Дисперсионные методы

Метод к — средних — переменные группируются в кластер в пределах порогового значения, которое задается исходя из определенного центра кластера.

Пример. 20 респондентов попросили выразить свое отношение к посещению торговых центров для приобретения товаров. Выделили шесть утверждений, степень согласия с которыми респондентов попросили выразить на основе семибалльной шкалы (1 — совсем не согласен, 7 — абсолютно согласен).

Fac_1 — Считаю посещение торговых центром приятным процессом.
Fac_2 — Посещение торговых центров подрывает бюджет моей семьи.
Fac_3 — Мне нравиться обедать и ужинать в торговых центрах.
Fac_4 — В торговых центрах мне нравиться делать хорошие покупки.
Fac_5 — Меня очень раздражает посещение торговых центров.
Fac_6 — Посещая разные магазины, можно сравнивать цены и выбирать более дешевый товар.

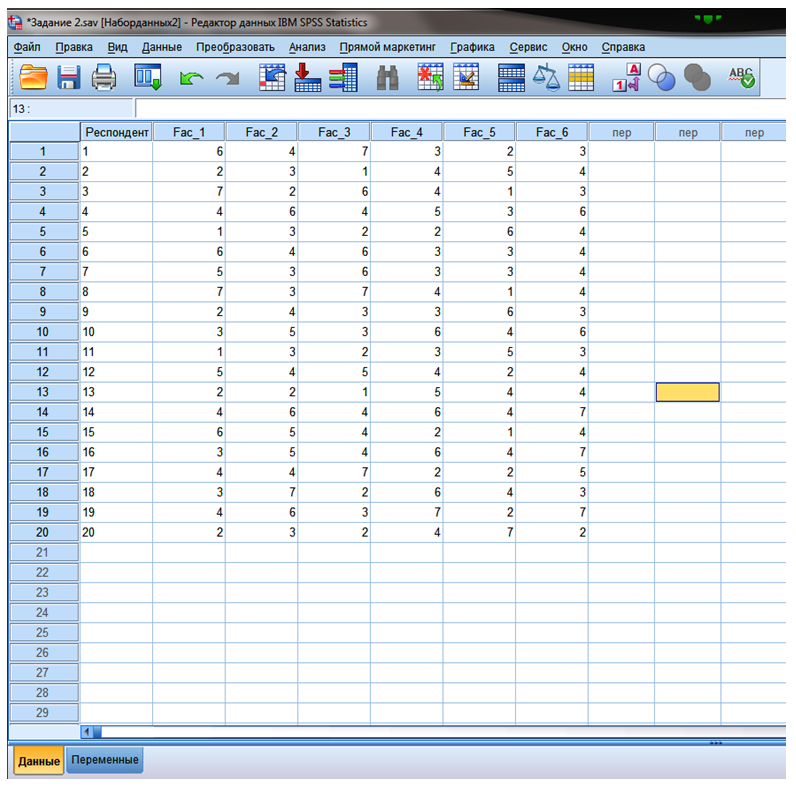
Рисунок 9.4 - Данные для кластеризации

Рисунок 9.4 - Данные для кластеризации

Вверх

Пошаговая инструкция

ШАГ 1. Подготовить данные для анализа в SPSS.

ШАГ 2. “Анализ” - выбрать “Классификация”. В рассматриваемом примере применяется иерархический кластерный анализ.

ШАГ 3. Анализ — Классификация — Иерархическая кластеризация - “Иерархический кластерный анализ” (Рисунок 9.5).

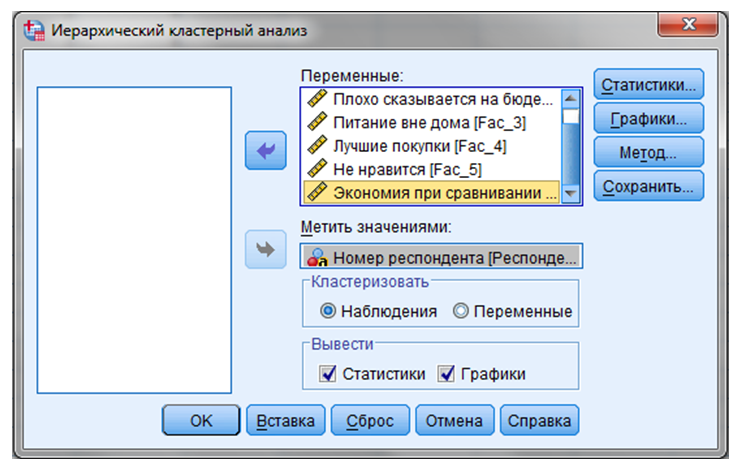
Рисунок 9.5 - Иерархический кластерный анализ

Рисунок 9.5 - Иерархический кластерный анализ

Выбираем все шесть факторов, отражающих отношение респондентов к посещению торговых центров, и переносим их в поле “Переменные”.

В поле “Метить значениями” необходимо перенести переменную “Номер респондента”. В данном случае могут использоваться только поле текстовые переменные, поэтому в столбце “Тип переменной” необходимо выбрать “Текстовая”.

В поле “Кластеризовать” выбрать один из двух предлагаемых вариантов: “Наблюдения” или “Переменные”. В нашем примере выбирается вариант “Наблюдения”, в ходе кластерного анализа будут собираться в кластеры потребители, а не характеристики их отношения.

ШАГ 4. Нажать кнопку “Статистики” - диалоговое окно “Статистические показатели”.

В окне “Статистические показатели” отметить команды “Порядок агломерации” и “Матрица близостей” (Рисунок 9.6).

Рисунок 9.6 — Диалоговое окно “Статистические показатели”

Рисунок 9.6 — Диалоговое окно “Статистические показатели”

В группе “Принадлежность к кластерам” можно выбрать три варианта:

Кнопка “Продолжить” - возвращаемся в основное диалоговое окно.

ШАГ 5. Кнопка “Графики” - на экране появляется вспомогательное диалоговое окно “Графики” (Рисунок 9.7).

Рисунок 9.7 - Диалоговое окно “Графики”

Рисунок 9.7 - Диалоговое окно “Графики”

В данном окне можно выбрать в качестве выводимых результатов анализа сосульчатую диаграмму, которая демонстрирует процесс формирования кластеров на основе величины разности между переменными.

Далее выбираем “Продолжить” - “Иерархический кластерный анализ”.

ШАГ 6. Кнопка “Метод” - позволяет нам работать с функциями окна “Методы” (Рисунок 9.8).

Рисунок 9.8 — Методы кластерного анализа

Рисунок 9.8 — Методы кластерного анализа

В поле “Метод” - выбрать метод “Варда”.

В поле “Мера” - выбрать интервальный показатель, по которому совокупность объектов исследования разделяется на кластеры.

Из предлагаемых программой интервальных показателей выбираем квадрат расстояния Евклида.

Кнопка “Продолжить” - “Иерархический кластерный анализ”.

ШАГ 7. Кнопка “Сохранить” - диалоговое окно “Сохранить”. В данном окне выбираем вариант сохранения результатов анализа в исходной базе данных. Выбираем кнопку “Диапазон решений” и устанавливаем диапазон от 3 до 5. В результате в конце списка переменных базы данных появятся новые переменные, которые были созданы в результате кластеризации. Данным переменным можно дать имена, которые соответствуют их общим характеристикам.

ШАГ 8. Кнопка “ОК”.

Интерпретация результатов

В таблице 9.2 “Шаги агломерации” показаны номера кластеров, которые объединяются на каждом этапе. В колонке “Коэффициенты” показаны эвклидовы расстояния между кластерами. В колонке “Следующий этап” показан шаг, на котором впервые был создан данный кластер.

С помощью данной таблицы можно провести предварительную оценку количества создаваемых кластеров, определив на каком этапе, резко возрастает евклидово расстояние между переменными.

Этап Кластер объединен с Коэффициенты Этап первого появления кластера Следующий этап
Кластер 1 Кластер 2 Кластер 1 Кластер 2
1 14 16 1,000 0 0 6
2 6 7 2,000 0 0 7
3 2 13 3,5000 0 0 15
4 5 11 5,000 0 0 11
5 3 8 6,500 0 0 16
6 10 14 8,167 0 1 9
7 6 12 10,500 2 0 10
8 9 20 13,000 0 0 11
9 4 10 15,583 0 6 12
10 1 6 18,500 0 7 13
11 5 9 23,000 4 8 15
12 4 19 27,750 9 0 17
13 1 17 33,100 10 0 14
14 1 15 41,333 13 0 16
15 2 5 51,833 3 11 18
16 1 3 64,500 14 5 19
17 4 18 79,667 12 0 18
18 2 4 172,667 15 17 19
19 1 2 328,600 16 18 0

Таблица 9.2 - Шаги агломерации

Следующим элементов окна вывода является древовидная диаграмма (рисунок 9.9). Данная диаграмма позволяет оценить расстояние между объектами и их принадлежность к кластерам на любом уровне.

Читать древовидную диаграмму нужно слева направо. Кластеры, которые объединяются в группу соединены вертикальными линиями. Шкала расстояний от 0 до 25 показывает величину квадрата расстояния Евклида, при которой кластеры объединяются. 0 — наименьшее расстояние первого этапа, 25 — наибольшее расстояние последнего этапа.

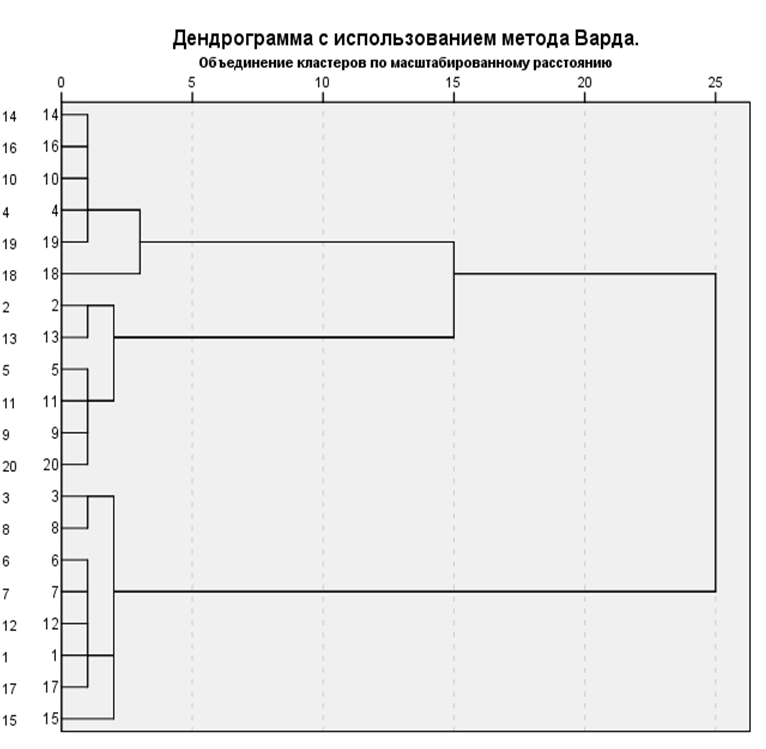
Рисунок 9.9 — Древовидная диаграмма

Рисунок 9.9 — Древовидная диаграмма

Для определения количества кластеров можно руководствоваться следующим:

Подсчитав частоты кластерной принадлежности, видно, что выбор трех кластеров приводит к кластерам, содержащим 8, 6 и 6 элементов, если же перейти к 4 — то размеры кластеров будут 8, 6, 5, 1.

Ward Method Приятный процесс Подрывает бюджет Питание вне дома Хорошие покупки Раздражение Экономия при сравнивании цен
1 Среднее 5,75 3,63 6,00 3,13 1,88 3,88
N 8 8 8 8 8 8
Стд.Отклонение 1,035 ,916 1,069 ,835 ,835 ,641
2 Среднее 1,67 3,00 1,83 3,50 5,50 3,33
N 6 6 6 6 6 6
Стд.Отклонение ,516 ,632 ,753 1,049 1,049 ,816
3 Среднее 3,50 5,83 3,33 6,00 3,50 6,00
N 6 6 6 6 6 6
Стд.Отклонение ,548 ,753 ,816 ,632 ,837 1,549
Итого Среднее 3,85 4,10 3,95 4,10 3,45 4,35
N 20 20 20 20 20 20
Стд.Отклонение 1,899 1,410 2,012 1,518 1,761 1,496

Таблица 9.3 — Результаты кластерного анализа

В таблице “Результаты кластерного анализа” выбираем переменные, включаемые в каждый из трех кластеров. В кластер 1 могут попасть респонденты, предпочитающие питаться вне дома и ответившие, что им нравиться посещать магазины (среднее 6,00 и 5,75). Следовательно, данный кластер можно назвать “любители торговых центров”. В данный кластер попадают переменные: 1, 3, 6, 7, 8, 12, 15 и 17. В кластер 2 попадают случаи 2, 5, 9, 11, 13 и 20, которые соответствуют варианту ответов, связанных с раздражением от торговых центров. Назовем его “раздраженные покупатели”. Кластер 3 можно назвать “экономные покупатели”, так как он имеет высокие средние показатели по факторам 2 (Подрывает бюджет), 4 (Хорошие покупки), 6 (Экономия при сравнивании цен).