10. Факторный анализ
Факторный анализ — представляет собой метод обобщения или сокращения большого количества переменных, объединение их в группы на основе характерных связей. В факторном анализе переменные не делятся на независимые и зависимые.
В практике маркетинговых исследований с факторный анализ применяется в следующих ситуациях
- для сегментирования рынка и выявления переменных с целью группировки потребителей;
- для определения характеристик торговой марки с целью выявления предпочтений потребителей;
- при разработке рекламной стратегии с целью выявления особенностей восприятия потребителем рекламного продукта
Факторный анализ применяется для выделения из большого массива данных малое число групп, состоящих из переменных, объединенных общими факторами (Рисунок 10.1).
Рисунок 10.1 –Диалоговое окно факторного анализа
В один фактор объединяются переменные, плотно коррелирующие между собой и слабо коррелирующие с переменными, которые объединяются на основе других факторов. Факторный анализ проводится с целью сокращения числа переменных и упрощение процедуры анализа существующей базы данных.
В процессе проведения факторного анализа рассчитываются и анализируются следующие показатели:
- Критерий сферичности Бартлетта — показатель, с помощью которого проверяют, отличаются ли корреляции от 0. Если г близко к нулю, то выбранная переменная не взаимосвязана с другими. Значимость меньше 0,05 указывает, на то что проведение факторного анализа приемлемо.
- Корреляционная матрица — матрица, включающая в себя все возможные коэффициенты корреляций r между анализируемыми перемнными.
- КМО — мера адекватности выборки Кайзера—Мейера—Олкина — величина, используемая для оценки применимости факторного анализа. Значения от 0,5 до 1 говорят об адекватности факторного анализа, значения до 0,5 указывают на то, что факторный анализ неприменим к выборке.
Графическое изображение критерия “каменистой осыпи” — график собственных значений факторов, расположенных в порядке убывания, используется для определения достаточного числа факторов.
Процедура факторного анализа включает следующие этапы:
- Формулировка проблемы.
- Проверка возможности проведения, вычисление корреляционной матрицы.
- Выбор метода факторного анализа.
- Извлечение факторов.
- Вращение факторов.
- Определение значений факторов.
- Проведение подгонки выбранной модели.
Пример. Проведем факторный анализ с целью сокращения массива данных, содержащих информацию о мотивах туристов, при выборе места отдыха за городом. Оптимизируем структуру данных, сократив число переменных.
Основные задачи:
- оценить возможность проведения и адекватность факторного анализа для данной выборки;
- вычислить корреляционную матрицу и выявить взаимосвязи между переменными базы данных;
- выявить и извлечь необходимое количество факторов для создания упрощенной структуры;
- разбить базу данных на группы факторов на основе значений совместной корреляции;
- подобрать названия созданным переменным.
Мотивы туристов, при выборе места отдыха за городом:
- близость к городу
- приемлемые цены
- близость водоема, леса
- уровень комфорта
- тишина, уединение
- хорошее питание
- наличие развлечений
- комфорт отдыха с детьми
- возможность лечения, ухода за здоровьем
Пошаговая инструкция
ШАГ 1. Меню “Анализ — Сокращение размерности — Факторный анализ ...”. Открывается диалоговое окно “Факторный анализ”.
ШАГ 2. Из этого списка переменных выбрать необходимый массив, и перенести его в поле “Переменные”.
Если есть необходимость провести факторный анализ отдельно для двух переменных, например мужчин и женщин, то в поле “Переменная отбора наблюдений” вносится переменная “пол”. В данном случае нет необходимости проводить такое деление.
ШАГ 3. Диалоговое окно “Описательные статистики— выбрать “КМО и критерий сферичности Бартлетта” для проведения тестов “КМО” и “Бартлетт”, проверяющих пригодность данных для проведения факторного анализа.
ШАГ 4. Диалоговое окно “Описательные статистики— “Корреляционная матрица— “Коэффициенты— “Продолжить”.
ШАГ 5. Диалоговое окно “Извлечение— задать условия определения количества факторов. В диалоговом окне “Извлечение— выбрать метод “Главные компоненты. — “Матрица корреляций” (Рисунок 10.2).
Рисунок 10.2 — Матрица корреляций
ШАГ 6. Задать условие: собственное значение больше “1”. При данном условии программа определит факторы в количестве больше 1.
ШАГ 7. Вывести график собственных значений — “График собственных значений— “Продолжить”.
ШАГ 8. Выбор ротации матрицы коэффициентов: в главном диалоговом окне “Факторный анализ— диалоговое окно “Вращение— метод ротации “Варимакс— “Продолжить”.
ШАГ 9. Создание новых переменных: в диалоговом окне “Факторный анализ— диалоговое окно “Значения факторов— отметить команду “Сохранить как переменные— метод расчета значений новых переменных “Регрессионная модель”. В итоге создаются новые переменные, которые можно будет использовать в дальнейшем анализе.
ШАГ 10. “ОК”.
Интерпретация результатов
- Величина КМО показывает приемлемую адекватность выборки для факторного анализа КМО = 0,512>0,5. Критерий Бартлетта (p<0,05), что говорит о целесообразности факторного анализа в силу коррелированности факторов.
- Выявление и извлечение необходимого количества факторов для создания упрощенной структуры
Компонента Начальные собственные значения Суммы квадратов нагрузок вращения Всего % дисперсии Кумулятивный % Всего % дисперсии Кумулятивный % 1 2,57 25,7 25,7 2,07 20,76 20,76 2 1,79 17,95 43,66 1,84 18,47 39,23 3 1,4 14,02 57,68 1,56 15,62 54,86 4 1,23 12,29 69,97 1,34 13,42 68,28 5 1,07 10,79 80,77 1,24 12,48 80,77 6 ,87 8,69 89,47 7 ,43 4,31 93,78 8 ,34 3,43 97,21 9 ,27 2,7 99,91 10 ,008 ,08 100,0 Метод выделения: Анализ главных компонент.
Начальные собственные значения должны быть больше 1.
Оптимальное число факторов — 5. Такая модель сохраняет 80,77% исходной информации, при этом число фактор сокращается в два раза.
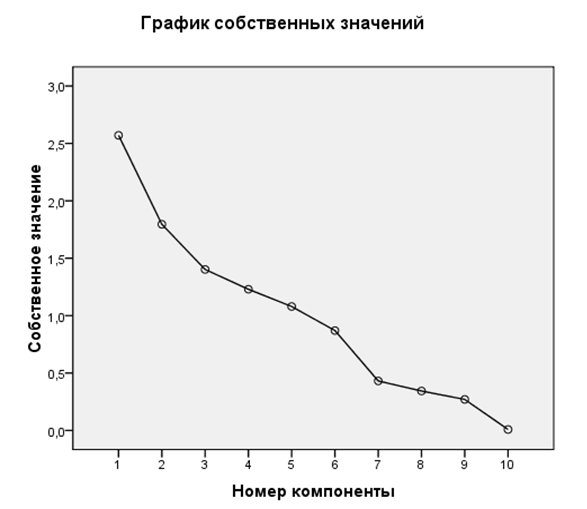
Рисунок 10.1 — График собственных значений
График показывает соответствующие собственные значения в системе координат: с 5 по 6 факторы происходит перелом графика. Это подтверждает, что оптимальное количество факторов 5.
- На основании ротированной матрицы (таблица 10.5) компонентов в одну группу собираются переменные, которые наиболее тесно взаимосвязанные между собой (наиболее высокое значение коэффициента корреляции). В результате программа группирует переменные исходного массива и создает матрицу преобразования компонент (таблица 10.6)
Компонента 1 2 3 4 5 близость к городу -,088 ,852 -,198 -,009 ,147 приемлемые цены ,278 -,190 -,221 -,561 ,622 близость водоема, леса ,074 -,240 -,210 ,664 ,215 уровень комфорта -,062 ,793 ,241 ,093 -,148 тишина, уединение ,988 -,074 ,082 -,040 -9,640E—6 хорошее питание ,059 ,331 ,831 ,158 ,054 наличие развлечений -,075 ,335 -,797 ,261 -,070 комфорт отдыха с детьми -,086 ,078 ,179 ,221 ,874 возможность лечения, ухода за здоровьем ,991 -,071 ,026 -,021 ,006 организация детского отдыха -,084 ,400 ,087 ,659 -,004 Таблица 10.5 — Матрица повернутых компонент
Метод выделения: Анализ методом главных компонент.
Метод вращения: Варимакс с нормализацией Кайзера.Компонента 1 2 3 4 5 1 -,69 ,61 ,023 ,36 -,12 2 ,55 ,48 ,64 ,19 ,03 3 ,45 ,35 ,75 ,32 ,002 4 -,101 -,008 ,000 ,14 ,98 ,020 ,51 -,130 -,83 ,123 Таблица 10.6 — Матрица преобразования компонент
Метод выделения: Анализ методом главных компонент.
Метод вращения: Варимакс с нормализацией Кайзера.Выделяем следующие факторы:
Фактор 1 — тишина и уединение, уход за здоровьем
Фактор 2 — близость к городу, уровень комфорта
Фактор 3 — хорошее питание, наличие развлечений
Фактор 4 — организация детского отдыха, близость водоем
Фактор 5 — комфорт отдыха с детьми, приемлемые цен - В базе данных автоматически переносятся новые переменные построенной факторной модели (Рисунок 10.2). В столбце “Метка” отображается номер компонента факторной модели.
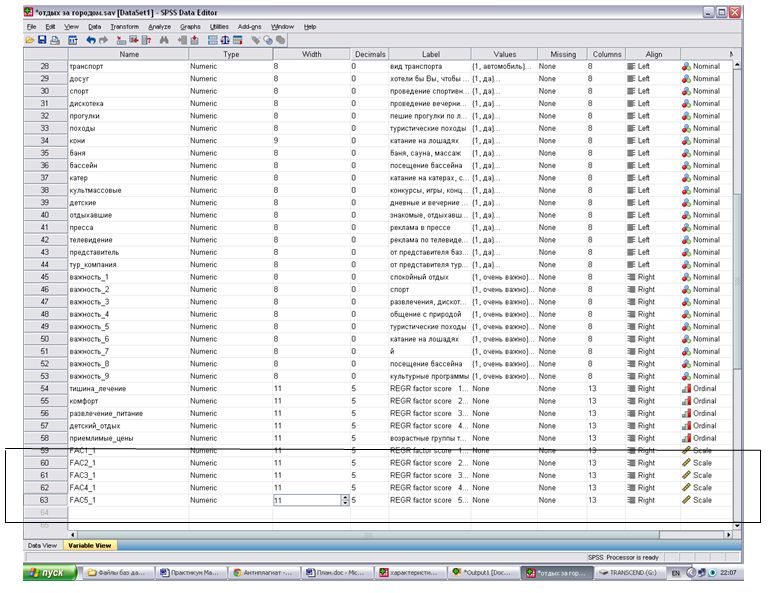
Рисунок 10.2 — Фрагмент вкладки “Переменные”
Названия новых компонент необходимо занести в исходную базу данных в столбец “Метка” таблицы “Переменные”, компьютер автоматически вычисляет значения новых переменных.
Суть новых переменных сводится к следующему: наибольшее отрицательное значение говорит о большей значимости переменной, и наоборот, наибольшее положительное значение говорит о наименьшей значимости переменной.
Созданные переменные в дальнейшем могут использоваться для анализа, например для проведения кластерного анализа.
| Мера адекватности и критерий Бартлетта | ||
|---|---|---|
| Мера выборочной адекватности Кайзера—Мейера—Олкина | ,512 | |
| Критерий сферичности Бартлетта | Приблиз. хи—квадрат | 262,3 |
| ст.св. | 45 | |
| Знч. | ,000 | |
Таблица 10.1 — Результаты теста КМО и Бартлетта
| близость к городу | приемлемые цены | близость водоема, леса | уровень комфорта | тишина, уединение | хорошее питание | наличие развлечений | комфорт отдыха с детьми | возможность лечения, ухода за здоровьем | организация детск. отдыха | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Корреляция | близость к городу | 1,000 | -,060 | ,009 | ,519 | -,172 | ,149 | ,322 | ,075 | -,166 | ,241 |
| приемлемые цены | -,060 | 1,000 | -,064 | -,341 | ,270 | -,247 | -,121 | ,232 | ,273 | -,407 | |
| близость водоема, леса | ,009 | -,064 | 1,000 | -,056 | ,017 | -,083 | ,107 | ,114 | ,027 | ,030 | |
| уровень комфорта | ,519 | -,341 | -,056 | 1,000 | -,113 | ,384 | ,070 | ,008 | -,125 | ,256 | |
| тишина, уединение | -,172 | ,270 | ,017 | -,113 | 1,000 | ,084 | -,167 | -,060 | ,989 | -,129 | |
| хорошее питани | ,149 | -,247 | -,083 | ,384 | ,084 | 1,000 | -,422 | ,191 | ,036 | ,237 | |
| наличие развлечений | ,322 | -,121 | ,107 | ,070 | -,167 | -,422 | 1,000 | -,045 | -,116 | ,248 | |
| комфорт отдыха с детьми | ,075 | ,232 | ,114 | ,008 | -,060 | ,191 | -,045 | 1,000 | -,053 | ,202 | |
| возможность лечения, ухода за здоровьем | -,166 | ,273 | ,027 | -,125 | ,989 | ,036 | -,116 | -,053 | 1,000 | -,106 | |
| организация детск. отдыха | ,241 | -,407 | ,030 | ,256 | -,129 | ,237 | ,248 | ,202 | -,106 | 1,000 | |
Таблица 10.2 — Корреляционная матрица.
Коэффициенты корреляции характеризуют плотность связи между переменными исходного массива.
